Notice
Recent Posts
Recent Comments
Link
| 일 | 월 | 화 | 수 | 목 | 금 | 토 |
|---|---|---|---|---|---|---|
| 1 | 2 | 3 | 4 | 5 | ||
| 6 | 7 | 8 | 9 | 10 | 11 | 12 |
| 13 | 14 | 15 | 16 | 17 | 18 | 19 |
| 20 | 21 | 22 | 23 | 24 | 25 | 26 |
| 27 | 28 | 29 | 30 |
Tags
- model_selection
- mysql설치 #mysql #mysqluser #mysqlworkbench
- sklearn
- allra
- fundbox
- 핀테크
- aarrr
- 역설구조
- 머신러닝
- 그로스해킹
- 활성화
- 전환율
- retention
- 올라
- BM분석
- pmf
- 한장으로끝내는비즈니스모델100
- 리텐션
- 퍼널분석
- 선정산서비스
- 바로팜
- 코호트
- 비즈니스모델
- 인게이지먼트
- 데이터분석
- CAC
- 팔방이익구조
- 서말리포켓
- 셀프스토리지
- activation
Archives
- Today
- Total
데이터로그😎
[지도학습] 1. 분류의 평가지표 본문
<분류(classification)의 성능평가 지표>
1. 정확도(accurcay)
2. 오차행렬(confusion matrix)
3. 정밀도(precision)
4. 재현율(recall)
5. F1 score
6. ROC AUC
0. 데이터 준비
- 암 데이터 받아오기
from sklearn.datasets import load_breast_cancer
import pandas as pd
import numpy as np
cancer = load_breast_cancer()
data = cancer.data
target = cancer.target
feature_names = cancer.feature_names
df = pd.DataFrame(data= data, columns = feature_names)
df['target'] = target
df
- target 변경
#cancer.target_names를 확인해보면 0: 암, 1: 종양이다.
# 모델 생성 목적을 암을 예측하기 위해서 만들 것이라서 종양을 0으로, 암을 1로 바꿔주기
tumor = df[df['target']==1].copy()
cancer = df[df['target']==0].copy()
tumor['target'] = 0
cancer['target'] = 1
sample = pd.concat([tumor, cancer[:30]], sort=True)
# 암 비율이 훨씬 적어야 하니까 cancer데이터는 30개까지만 합쳐주기
sample['target'].value_counts()- 데이터 분할 & 모델정의 & 학습
from sklearn.model_selection import train_test_split
from sklearn.linear_model import LogisticRegression
# LogisticRegression은 회귀라는 이름이 붙어있지만 사실은 분류이다.
X_train, X_test, y_train, y_test = train_test_split(
sample.drop('target',axis=1),
sample['target'],
random_state = 42
)
model = LogisticRegression(max_iter = 10000) #max_iter = 최대반복횟수
model.fit(X_train, y_train)
lr_pred = model.predict(X_test)1. 정확도(accuracy)
from sklearn.metrics import accuracy_score
accuracy_score(y_test, lr_pred)
>>>결과: 0.9690721649484536그러나..정확도로 모델을 평가하면 아래와 같은 상황이 발생할 수도 있다.
- 돌팔이 曰 "암인 사람도 어차피 많이 없는데 그냥 모든 암검사 한 사람한테 결과가 종양이라고 해볼까?”
dolpal_pred = np.zeros(shape=y_test.shape)
>>>
array([0., 0., 0., 0., 0., 0., 0., 0., 0., 0., 0., 0., 0., 0., 0., 0., 0.,
0., 0., 0., 0., 0., 0., 0., 0., 0., 0., 0., 0., 0., 0., 0., 0., 0.,
0., 0., 0., 0., 0., 0., 0., 0., 0., 0., 0., 0., 0., 0., 0., 0., 0.,
0., 0., 0., 0., 0., 0., 0., 0., 0., 0., 0., 0., 0., 0., 0., 0., 0.,
0., 0., 0., 0., 0., 0., 0., 0., 0., 0., 0., 0., 0., 0., 0., 0., 0.,
0., 0., 0., 0., 0., 0., 0., 0., 0., 0., 0., 0.])accuracy_score(y_test, dolpal_pred)
>>0.9072164948453608엉터리 데이터인데도 정확도가 90%가 넘는다니…!
따라서 정확도만 보고 성능을 판단하는 것은 위험하다. 더 세밀한 지표가 필요!!
→ 오차행렬 & 정밀도 & 정확도
2. 오차행렬( 혼돈행렬, confusion matrix)
| Predicted Negative | Predicted Positive | |
| Actual Negative | True Negative (TN) | False Positive (FP) |
| Actual Positive | False Negative (FN) | True Positive (TP) |
from sklearn.metrics import confusion_matrix
# LogisticRegression의 혼동행렬
lr_conf_matrix = confusion_matrix(y_test, lr_pred)
print('모델의 오차행렬: \n{}'.format(lr_conf_matrix))
>>결과:
모델의 오차행렬:
[[87 1]
[ 2 7]]- 해석
- TN(실제로 암 X 진단: 암 X)=87
- FN (실제로 암 O 진단: 암 X) =2
- FP (실제 암 X 진단: 암O) = 1
- TP(실제 암 O 진단 암O) = 7
- FN(2)을 낮추는 방식으로 성능을 올려야 함
- 여기서.. 돌팔이의 오차행렬은 어떨까?
- 돌팔이의 오차행렬은 1로 예측(암이라고 예측)한 것이 하나도 없음 (FP=0, TP=0)
- FN이 9나 되어버림. (암인데 암이 아니라고 한 것)
# 돌팔이의 혼동 행렬
dolpal_conf_matrix = confusion_matrix(y_test, dolpal_pred)
print('돌팔이의 오차행렬: \n{}'.format(dolpal_conf_matrix))
>>결과:
돌팔이의 오차행렬:
[[88 0]
[ 9 0]]
- 오차행렬 heatmap
import matplotlib.pyplot as plt
import seaborn as sns
plt.figure(figsize=(12, 5))
plt.subplot(121)
ax = sns.heatmap(
lr_conf_matrix,
annot=True,
cmap="Reds"
)
ax.set_title("model's confusion matrix")
plt.subplot(122)
ax = sns.heatmap(
dolpal_conf_matrix,
annot=True,
cmap="Reds",
)
ax.set_title("dolpal's confusion matrix")
plt.xlabel("Predict")
plt.ylabel("Actual")
plt.show()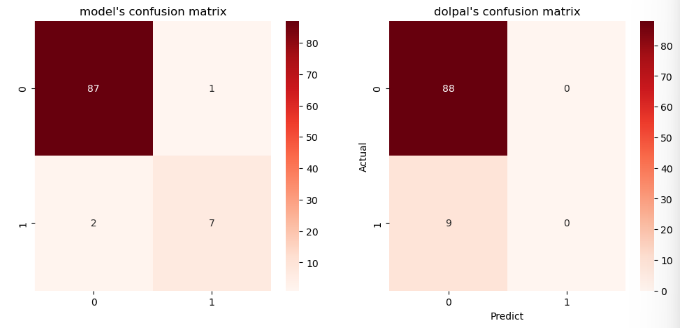
3. 정밀도(precision) & 재현율(recall)
3-1. 정밀도, 재현율이란?
- 업무 특성상 정밀도 or 재현율을 강조해야 하는경우 , threshold를 조정해 수치를 조정할 수 있음
- 두 지표 모두 높게 얻는게 best!!
- 그러나 정밀도/재현율은 trade-off관계라서 하나가 올라가면 하나가 떨어지기 쉬움. 조심.
정밀도재현율 (민감도, TPR)공식의미어떤 경우 사용?예시초점
| 정밀도 | 재현율(민감도, TPR) | |
| 공식 | TP/(FP+TP) | TP/(FN+TP) |
| 의미 | - 예측을 Positive로 한 값 중에서 예측값과 실제값이 일치한 데이터 비율 - 예측을 Positive로 한 값(TP+FP) 중 실제 값이 Positive인 경우(TP) - Positive 예측 성능을 더욱 정밀하게 측정하는 지표 |
실제로 Positive인 값 중에 예측값이 Positive였던 값 = 모델이 실제 양성인 샘플을 얼마나 잘 찾아내는지. |
| when to use? | FP가 중요한 경우 (실제 Positive인데 Negative로 잘못예측한 경우) | FN이 중요한 경우 (실제 Positive인데 Negative음성으로 잘못 판단한 경우) |
| 예시 | 스팸메일이 아닌데 스팸메일이라고 분류한 경우(업무차질) | 암인데 암아니라고 판단 |
| 초점 | FP 낮추기 | FN 낮추기 |
- 정밀도, 재현율 구하기
from sklearn.metrics import precision_score, recall_score
print('정밀도:{:.3f}'.format(precision_score(y_test, lr_pred))
print('재현율:{:.3f}'.format(recall_score(y_test, lr_pred))
>>정밀도: 0.875
재현율: 0.778
# 재현율이 더 낮음. 따라서 재현율 높여야함.
3-2. 사이킷런의 predict_proba()
- predict_proba: 각 클래스에 대한 예측 확률을 확인.
- predict()가 수행될 때 predict_proba가 먼저 수행되고 담에 예측값이 결정된다고 보면 됨.
- sklearn의 분류 알고리즘이 확률을 구하는 과정
- 개별 레이블로 결정 확률 구함
- 레이블 중 예측 확률이 큰 레이블값으로 예측을 함
- 이러한 개별 레이블의 예측 확률을 반환하는 메소드가 predict_proba임
lr_pred_proba = model.predict_proba(X_test) #예측확률
lr_pred = model.predcit(X_test) # 예측결과
print(lr_pred_proba[:3])
print()
print(lr_pred[:3])
>>[[9.99277955e-01 7.22045316e-04]
[9.99317729e-01 6.82270968e-04]
[9.99999986e-01 1.35283319e-08]]
[0 0 0]
#해석
[9.99277955e-01 7.22045316e-04] 둘 중에 target이 0인 수가 높음. 따라서
[0 0 0]에서 첫번째 데이터가 0인 것임
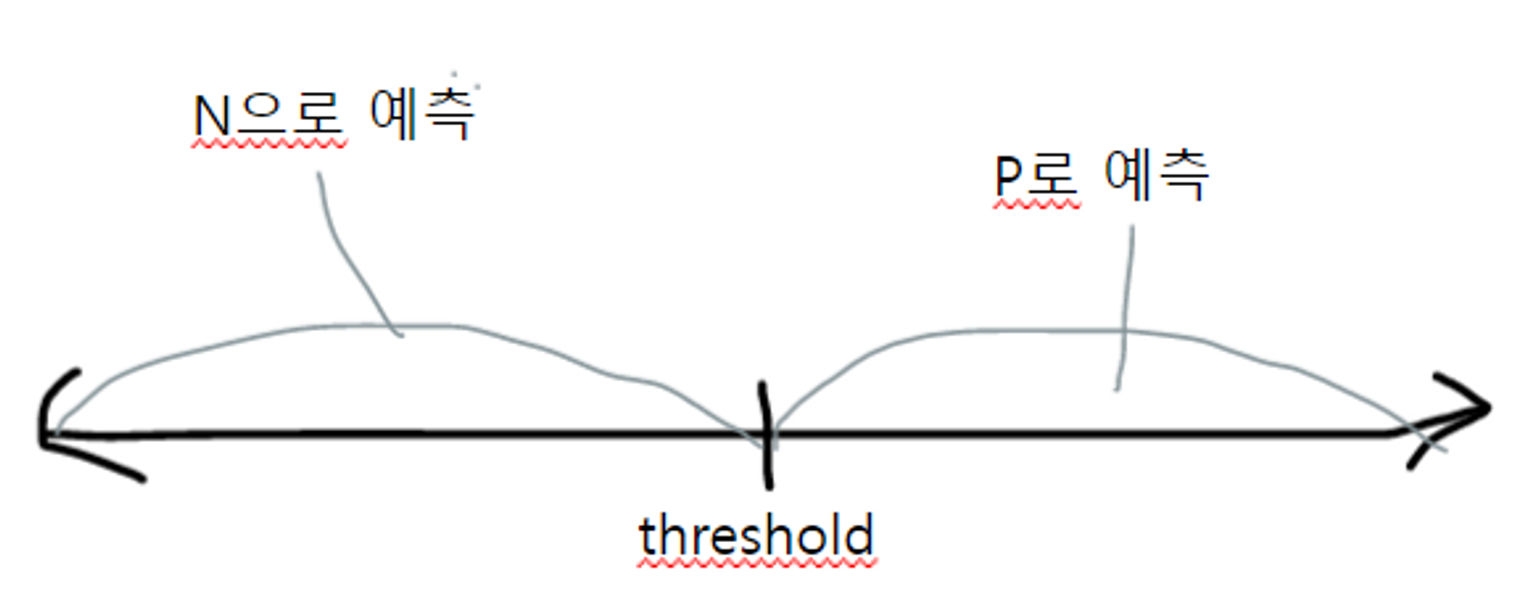
3-3. Binarizer클래스를 통해 threshold 조절하기
- Binarizer: 임계값(threshold)를 기준으로 입력 데이터를 0 또는 1의 이진(binary) 데이터로 변환하는 변환기(transformer).
- 이진 분류문제에서 모델의 출력을 이진화할 때 주로 사용.
- default threshold = 0.5
- threshold ↓ : P로 예측될 확률(FP ↑), N으로 예측될 확률(FN↓ ) ⇒ 재현율이 높아짐
- threshold ↑ : P로 예측될 확률(FP ↓), N으로 ㅇ예측될 확률(FN↑)) ⇒ 재현율 낮아짐
from sklearn.preprocessing import Binarizer
#임계값=0.5일때 오차행렬
# 사실 따로 binarizer로 임계값 설정하지 않아도 됨.why?기본이 0.5니까
binarizer = Binarizer(threshold=0.5)
# predict_proba() 반환값의 두번째 칼럼, 즉 Positive 클래스 칼럼만 추출해 Binarizer적용
lr_pred_proba_1 = model.predict_proba(X_test)[:,1].reshape(-1,1)
custom_predict = binarizer.fit_transform(lr_pred_proba_1)
- model.predict_proba(X_test)결과
- 인덱스[0][0],[1][0],[2][0]...은 target이 0일 때를 의미 = tumor
- 인덱스[0][1],[1][1],[2][1]…은 target이 1일때를 의미 = cancer
array([[9.99277955e-01, 7.22045316e-04],
[9.99317729e-01, 6.82270968e-04],
[9.99999986e-01, 1.35283319e-08],
[9.99971619e-01, 2.83811234e-05],
[9.99999999e-01, 1.33687847e-09],
[9.99972012e-01, 2.79882348e-05],
.........
[1.00000000e+00, 2.78828346e-11],
[9.99973593e-01, 2.64071385e-05],
[9.99999671e-01, 3.29157646e-07]])
- custom_predict 결과
- fit_trasform()메소드는 입력된 narray의 값을 지정된 threshold(여기서는 0.5)보다 같거나 작으면 0, 크면 1값으로 반환. 즉 1로 나온건 암이라는 것
array([[0.],
[0.],
[0.],
[0.],
[0.],
[0.],
[0.],
[0.],
[0.],
[0.],
[0.],
[0.],
[0.],
[0.],
[1.],
[0.],
.....
- 결과를 히트맵으로 그려보기
import matplotlib.pyplot as plt
import seaborn as sns
from sklearn.metrics import accuracy_score, precision_score , recall_score , confusion_matrix
def get_clf_eval(y_test, pred, ax=None):
confusion = confusion_matrix( y_test, pred)
precision = precision_score(y_test , pred)
recall = recall_score(y_test , pred)
accuracy = accuracy_score(y_test, pred)
hmap_ax = sns.heatmap(
confusion,
annot=True,
cmap="Reds",
ax=ax
)
hmap_ax.set_title('A: {0:.4f}, P: {1:.4f}, R: {2:.4f}'.format(accuracy , precision ,recall))get_clf_eval(y_test, custom_predict)
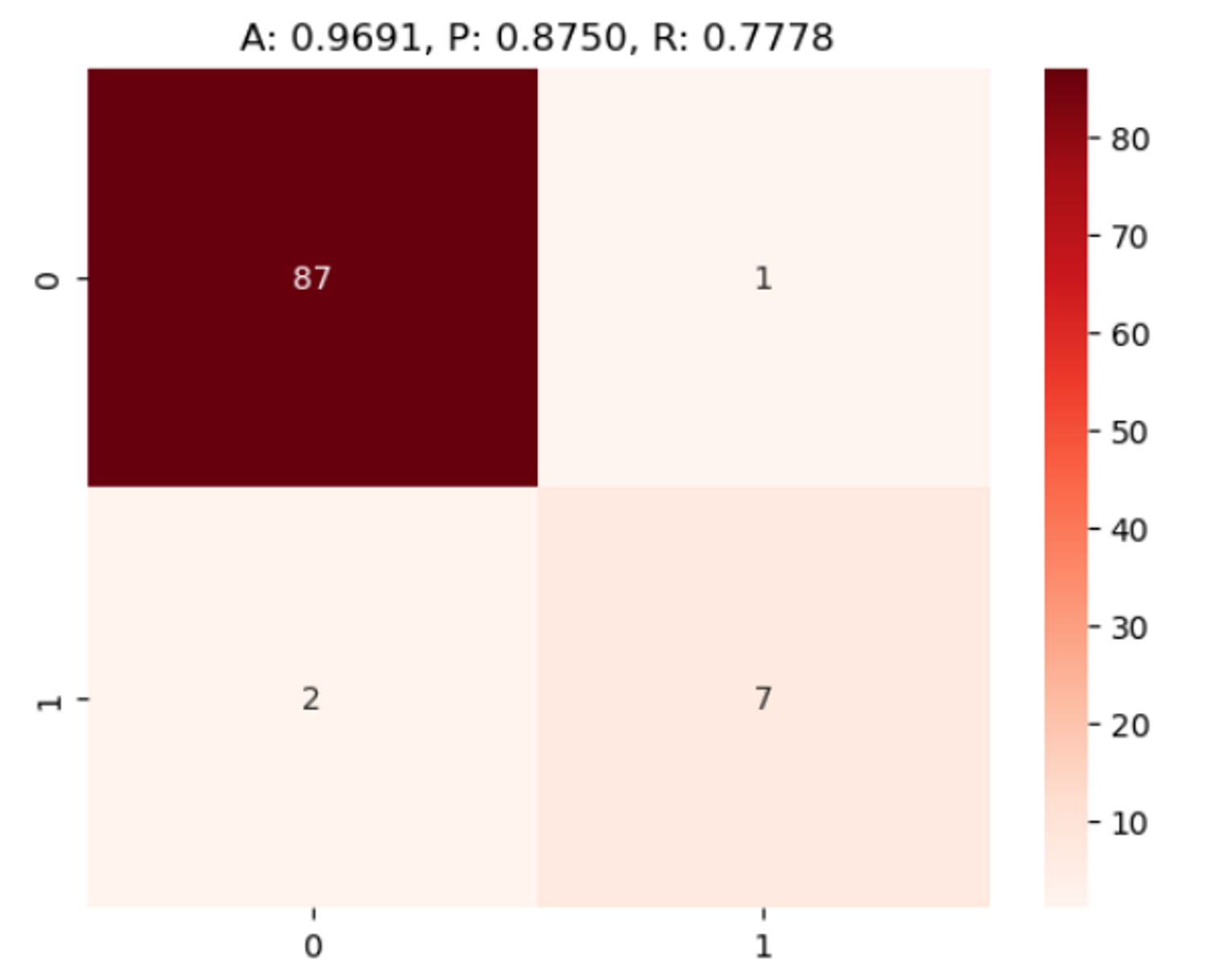
*정밀도:0.88%, 재현율: 0.78% → 재현율을 높여야 함 → threshold낮춰야
- Threshold 변화 시 정확도, 재현율, 정밀도 어케 변하는가?
# threshold = 0.1일 때
binarizer = Binarizer(threshold=0.1)
custom_predict = binarizer.fit_transform(lr_pred_proba_1)
get_clf_eval(y_test, custom_predict)
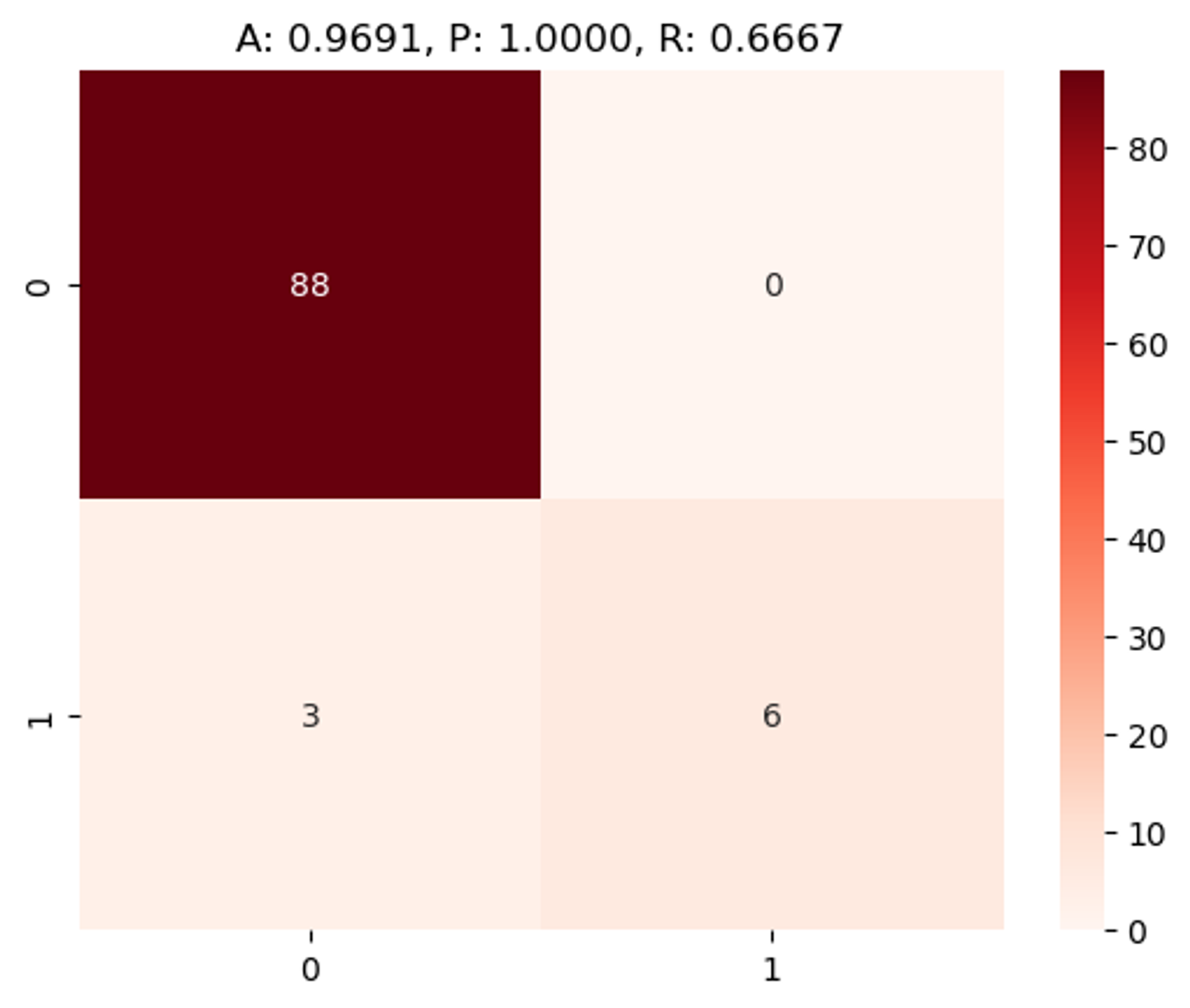
# threshold = 0.8일 때
binarizer = Binarizer(threshold=0.8)
custom_predict = binarizer.fit_transform(lr_pred_proba_1)
get_clf_eval(y_test, custom_predict)
# threshold=0.1,0.5일때보다 재현율(R) 낮아짐.
3-4. precision_recall_curve
The precision_recall_curve function returns three arrays:
precision_recall_curve는 precision, recall, thresholds 행렬을 각각 반환함. (1차원)/ threshold는 자동으로 설정됨.(가능한 모든 threshold에서 정밀도,재현율 계산)
precision.shape = (97,0), recall.shape=(97,0), thresholds.shape=(96,0)
- precision: An array of precision values, corresponding to the thresholds at which the precision was calculated.
- recall: An array of recall values, corresponding to the thresholds at which the recall was calculated.
- thresholds: An array of probability thresholds used to calculate precision and recall.
import matplotlib.pyplot as plt
import matplotlib.ticker as ticker
from sklearn.metrics import precision_recall_curve
def precision_recall_curve_plot(y_test , pred_proba_c1):
# threshold ndarray와 이 threshold에 따른 정밀도, 재현율 ndarray 추출.
precisions, recalls, thresholds = precision_recall_curve( y_test, pred_proba_c1)
# X축을 threshold값으로, Y축은 정밀도, 재현율 값으로 각각 Plot 수행. 정밀도는 점선으로 표시
plt.figure(figsize=(8,6))
threshold_boundary = thresholds.shape[0]
plt.plot(thresholds, precisions[0:threshold_boundary], linestyle='--', label='precision')
plt.plot(thresholds, recalls[0:threshold_boundary],label='recall')
# x축, y축 label과 legend, 그리고 grid 설정
plt.xlabel('Threshold value')
plt.ylabel('Precision and Recall value')
plt.legend()
plt.grid()
plt.show()
precision_recall_curve_plot( y_test, model.predict_proba(X_test)[:, 1] )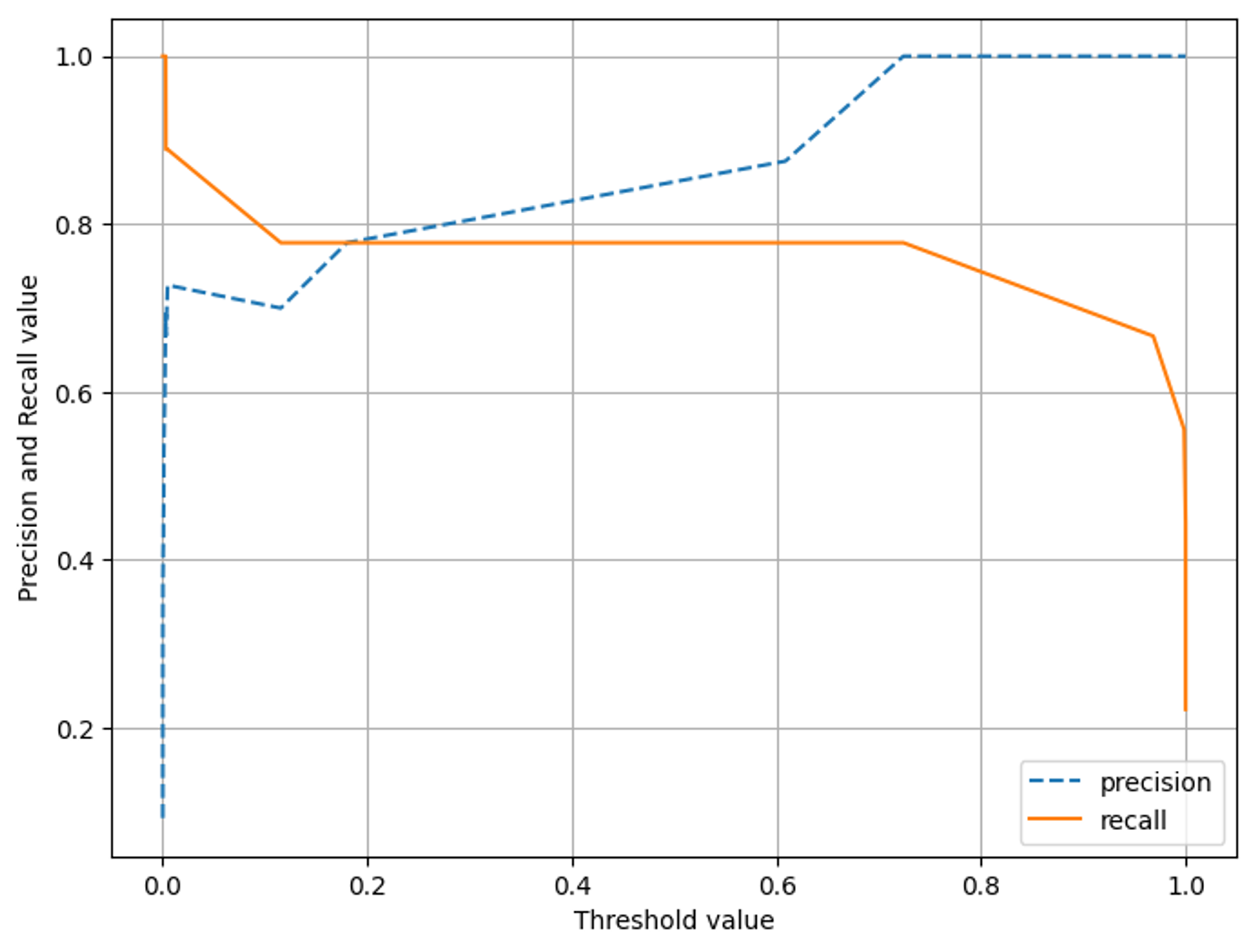
4. F1 Score
- 정밀도와 재현율을 결합한 지표
from sklearn.metrics import f1_score
f1 = f1_score(y_test, lr_pred)
f1
5. ROC 곡선
- 머신러닝 이진 분류 모델의 예측 성능을 판단하는 중요한 평가 지표
- FPR을 0~1로 변경하면서 TPR(재현율)변화값 구함
- 어떻게 FPR변화? 임곗값을 변화시키면 됨
- FPR(False Positive Rate)가 변할 때 TPR(True Positive Rate)가 어떻게 변하는지를 나타내는 곡선이다.
- TPR = 재현율 = TP/(TP+FN)=민감도= 실제값 positive가 정확히 예측되어야 하는 수준
- TNR = 특이성 = TN/(TN+FP) = True Negative Rate = 실제값 negative가 정확히 예측돼야 하는 수준
- FPR = 1-TNR = FP/(FP+TN) = 실제로 음성인 데이터 중에서 음성을 양성으로 잘못 예측한 비율
- FPR을 0으로 만드는 법?
- 임계값을 1로 지정하면됨
- 임계값이 1 → 아예 Positive로 예측하지 않음 → FP가 0이 됨 → FPR 0
- 임계값을 1로 지정하면됨
- FPR을 1로 만드는 법?
- 임계값을 0으로 지정하면 됨
- 임계값 0 → 아예 Negative로 예측 x → FPR = FP/FP = 1
- 임계값을 0으로 지정하면 됨
- roc_curve()
- 입력 파라미터:
- y_true: 실제 클래스 값 (y_test)
- y_score: predict_proba()반환값중 Positive 칼럼
- 입력 파라미터:
- roc_curve는 FPR, TPR, threshold 반환함.
- FPR: 1 - Specificity, 거짓 양성 비율, (FP / (FP + TN))
- TPR: Recall, 진짜 양성 비율, (TP / (TP + FN))
- thresholds: 임계값, 분류 결정 임계값을 ndarray로 반환합니다.
from sklearn.metrics import roc_curve
def roc_curve_plot(y_test , pred_proba_c1):
# 임곗값에 따른 FPR, TPR 값을 반환 받음.
fprs , tprs , thresholds = roc_curve(y_test ,pred_proba_c1)
# ROC Curve를 plot 곡선으로 그림.
plt.plot(fprs , tprs, label='ROC')
# 가운데 대각선 직선을 그림.
plt.plot([0, 1], [0, 1], 'k--', label='Random')
# FPR X 축의 Scale을 0.1 단위로 변경, X,Y 축명 설정등
start, end = plt.xlim()
plt.xticks(np.round(np.arange(start, end, 0.1),2))
plt.xlim(0,1); plt.ylim(0,1)
plt.xlabel('FPR( 1 - Sensitivity )'); plt.ylabel('TPR( Recall )')
plt.legend()
plt.show()
roc_curve_plot(y_test, model.predict_proba(X_test)[:, 1] )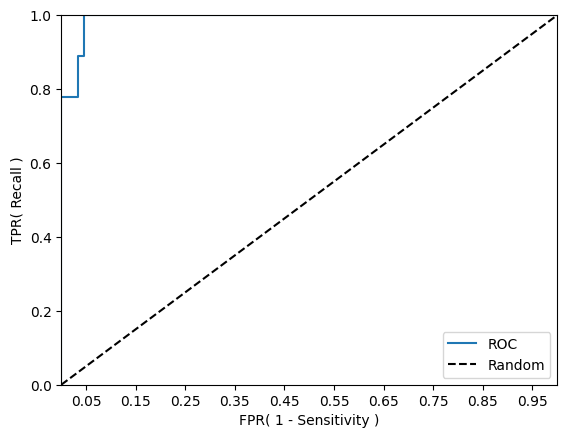
from sklearn.metrics import roc_auc_score
# roc auc 성능 수치 반환
pred_proba = model.predict_proba(X_test)[:, 1]
roc_score = roc_auc_score(y_test, pred_proba)
print('ROC AUC 값: {0:.4f}'.format(roc_score))'#4. 기타 공부 > #4.2. 머신러닝' 카테고리의 다른 글
| [지도학습] 2. Decision Tree (1) | 2023.09.04 |
|---|---|
| [지도학습] 0. 분류(Classification) (0) | 2023.09.04 |
| 데이터 전처리 (0) | 2023.09.03 |
| model_selection 모듈 (1) | 2023.09.03 |
| 머신러닝의 분류 (0) | 2023.08.30 |



